square holes

If you like handy work and tools and sawdust and grease you might have already considered what the best method for making square holes is. This depends on many things like the material, the size of the hole and your budget. With a good budget, a not too large hole and some appreciation for mathematics you will find the method described in this entry to be the coolest.
Reuleaux Triangle
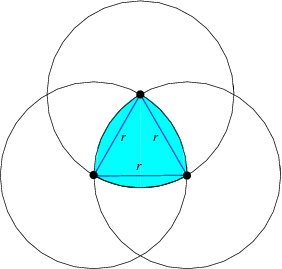The fat triangle formed from the intersection of three circles with origins at the vertices of an equilateral triangle is the Reuleaux Triangle. Interestingly it has the same maximum width regardless of how it is rotated. this property was thought to be only possessed by circles once and yet here's a simple and apt counter example.

Constant width shapes can make great manhole covers, as no orientation of the cover will let it fall through the manhole. A few years ago Microsoft interviewers asked job applicants why manhole covers were round and this was thought to be one of the best answers. Another more important property of constant width shapes is that they can rotate inside parallel lines.

Rotation of a Reuleaux Triangle is possible inside a square and it can encompase almost all the area of said square with the proper parameters.
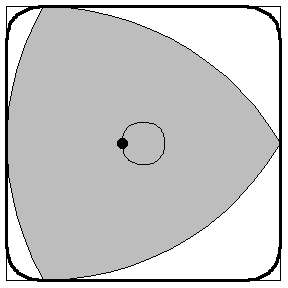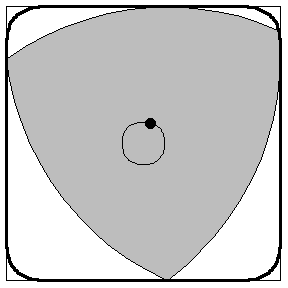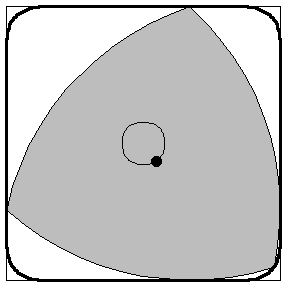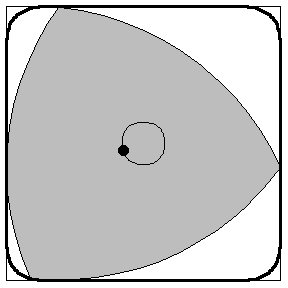This shape created by the rotating reuleaux is about 99% the size of the theoretical square it is trying to reproduce. Using a triangle like this a drill bit can be made to drill nearly square holes. The difficulty lies in reproducing the path that the centroid of the R.triangle travels in a real tool. It can be closely approximated by a superellipse |X|^r+|Y|^r= a^r and thanks to Harry Watt you can go by the special drill.

the actual drillbit looks like this

 

With concave parts to be able to cut into the material. You can also do cool things like this to get linear alternating motion from circular continuous.

one of the most interesting applications of Reuleaux triangles is the Wankel engine:

 

source